Note
Go to the end to download the full example code.
BrainGlobe Atlas API#
Using the BrainGlobe Atlas API to fetch and inspect an atlas
Import the Atlas API and find an atlas#
Import the API and some other tools
from brainglobe_atlasapi import BrainGlobeAtlas
from pprint import pprint # to format printed data nicely
import numpy as np
from matplotlib import pyplot as plt
from matplotlib import colormaps as cm
To know what atlases are available through BrainGlobe, we can use the show_atlases function (requires an internet connection):
from brainglobe_atlasapi import show_atlases
show_atlases()
╭───────────────────────────── Brainglobe Atlases ─────────────────────────────╮
│ Local Latest │
│ Name Download… Updated version version │
│ admba_3d_e11_5_mouse_16um 1.1 │
│ admba_3d_e13_5_mouse_16um 1.1 │
│ admba_3d_e15_5_mouse_16um 1.1 │
│ admba_3d_e18_5_mouse_16um 1.1 │
│ admba_3d_p14_mouse_16.752um 1.1 │
│ admba_3d_p28_mouse_16.752um 1.1 │
│ admba_3d_p4_mouse_16.752um 1.1 │
│ admba_3d_p56_mouse_25um 1.1 │
│ african_molerat_20um 1.1 │
│ allen_cord_20um 1.2 │
│ allen_human_500um 1.0 │
│ allen_mouse_100um 1.2 │
│ allen_mouse_10um 1.2 │
│ allen_mouse_25um 1.2 │
│ allen_mouse_50um 1.2 │
│ allen_mouse_bluebrain_barrels_1… 1.0 │
│ allen_mouse_bluebrain_barrels_2… 1.0 │
│ australian_mouse_15um 1.0 │
│ azba_zfish_4um 1.2 │
│ carea_mouse_25um 1.1 │
│ ccfv3augmented_mouse_10um 1.0 │
│ ccfv3augmented_mouse_25um 1.0 │
│ columbia_cuttlefish_50um 1.0 │
│ csl_cat_500um 1.0 │
│ demba_allen_seg_dev_mouse_p10_2… 1.0 │
│ demba_allen_seg_dev_mouse_p10_2… 1.0 │
│ demba_allen_seg_dev_mouse_p11_2… 1.0 │
│ demba_allen_seg_dev_mouse_p11_2… 1.0 │
│ demba_allen_seg_dev_mouse_p12_2… 1.0 │
│ demba_allen_seg_dev_mouse_p12_2… 1.0 │
│ demba_allen_seg_dev_mouse_p13_2… 1.0 │
│ demba_allen_seg_dev_mouse_p13_2… 1.0 │
│ demba_allen_seg_dev_mouse_p14_2… 1.0 │
│ demba_allen_seg_dev_mouse_p14_2… 1.0 │
│ demba_allen_seg_dev_mouse_p15_2… 1.0 │
│ demba_allen_seg_dev_mouse_p15_2… 1.0 │
│ demba_allen_seg_dev_mouse_p16_2… 1.0 │
│ demba_allen_seg_dev_mouse_p16_2… 1.0 │
│ demba_allen_seg_dev_mouse_p17_2… 1.0 │
│ demba_allen_seg_dev_mouse_p17_2… 1.0 │
│ demba_allen_seg_dev_mouse_p18_2… 1.0 │
│ demba_allen_seg_dev_mouse_p18_2… 1.0 │
│ demba_allen_seg_dev_mouse_p19_2… 1.0 │
│ demba_allen_seg_dev_mouse_p19_2… 1.0 │
│ demba_allen_seg_dev_mouse_p20_2… 1.0 │
│ demba_allen_seg_dev_mouse_p20_2… 1.0 │
│ demba_allen_seg_dev_mouse_p21_2… 1.0 │
│ demba_allen_seg_dev_mouse_p21_2… 1.0 │
│ demba_allen_seg_dev_mouse_p22_2… 1.0 │
│ demba_allen_seg_dev_mouse_p22_2… 1.0 │
│ demba_allen_seg_dev_mouse_p23_2… 1.0 │
│ demba_allen_seg_dev_mouse_p23_2… 1.0 │
│ demba_allen_seg_dev_mouse_p24_2… 1.0 │
│ demba_allen_seg_dev_mouse_p24_2… 1.0 │
│ demba_allen_seg_dev_mouse_p25_2… 1.0 │
│ demba_allen_seg_dev_mouse_p25_2… 1.0 │
│ demba_allen_seg_dev_mouse_p26_2… 1.0 │
│ demba_allen_seg_dev_mouse_p26_2… 1.0 │
│ demba_allen_seg_dev_mouse_p27_2… 1.0 │
│ demba_allen_seg_dev_mouse_p27_2… 1.0 │
│ demba_allen_seg_dev_mouse_p28_2… 1.0 │
│ demba_allen_seg_dev_mouse_p28_2… 1.0 │
│ demba_allen_seg_dev_mouse_p29_2… 1.0 │
│ demba_allen_seg_dev_mouse_p29_2… 1.0 │
│ demba_allen_seg_dev_mouse_p30_2… 1.0 │
│ demba_allen_seg_dev_mouse_p30_2… 1.0 │
│ demba_allen_seg_dev_mouse_p31_2… 1.0 │
│ demba_allen_seg_dev_mouse_p31_2… 1.0 │
│ demba_allen_seg_dev_mouse_p32_2… 1.0 │
│ demba_allen_seg_dev_mouse_p32_2… 1.0 │
│ demba_allen_seg_dev_mouse_p33_2… 1.0 │
│ demba_allen_seg_dev_mouse_p33_2… 1.0 │
│ demba_allen_seg_dev_mouse_p34_2… 1.0 │
│ demba_allen_seg_dev_mouse_p34_2… 1.0 │
│ demba_allen_seg_dev_mouse_p35_2… 1.0 │
│ demba_allen_seg_dev_mouse_p35_2… 1.0 │
│ demba_allen_seg_dev_mouse_p36_2… 1.0 │
│ demba_allen_seg_dev_mouse_p36_2… 1.0 │
│ demba_allen_seg_dev_mouse_p37_2… 1.0 │
│ demba_allen_seg_dev_mouse_p37_2… 1.0 │
│ demba_allen_seg_dev_mouse_p38_2… 1.0 │
│ demba_allen_seg_dev_mouse_p38_2… 1.0 │
│ demba_allen_seg_dev_mouse_p39_2… 1.0 │
│ demba_allen_seg_dev_mouse_p39_2… 1.0 │
│ demba_allen_seg_dev_mouse_p40_2… 1.0 │
│ demba_allen_seg_dev_mouse_p40_2… 1.0 │
│ demba_allen_seg_dev_mouse_p41_2… 1.0 │
│ demba_allen_seg_dev_mouse_p41_2… 1.0 │
│ demba_allen_seg_dev_mouse_p42_2… 1.0 │
│ demba_allen_seg_dev_mouse_p42_2… 1.0 │
│ demba_allen_seg_dev_mouse_p43_2… 1.0 │
│ demba_allen_seg_dev_mouse_p43_2… 1.0 │
│ demba_allen_seg_dev_mouse_p44_2… 1.0 │
│ demba_allen_seg_dev_mouse_p44_2… 1.0 │
│ demba_allen_seg_dev_mouse_p45_2… 1.0 │
│ demba_allen_seg_dev_mouse_p45_2… 1.0 │
│ demba_allen_seg_dev_mouse_p46_2… 1.0 │
│ demba_allen_seg_dev_mouse_p46_2… 1.0 │
│ demba_allen_seg_dev_mouse_p47_2… 1.0 │
│ demba_allen_seg_dev_mouse_p47_2… 1.0 │
│ demba_allen_seg_dev_mouse_p48_2… 1.0 │
│ demba_allen_seg_dev_mouse_p48_2… 1.0 │
│ demba_allen_seg_dev_mouse_p49_2… 1.0 │
│ demba_allen_seg_dev_mouse_p49_2… 1.0 │
│ demba_allen_seg_dev_mouse_p4_20… 1.0 │
│ demba_allen_seg_dev_mouse_p4_25… 1.0 │
│ demba_allen_seg_dev_mouse_p50_2… 1.0 │
│ demba_allen_seg_dev_mouse_p50_2… 1.0 │
│ demba_allen_seg_dev_mouse_p51_2… 1.0 │
│ demba_allen_seg_dev_mouse_p51_2… 1.0 │
│ demba_allen_seg_dev_mouse_p52_2… 1.0 │
│ demba_allen_seg_dev_mouse_p52_2… 1.0 │
│ demba_allen_seg_dev_mouse_p53_2… 1.0 │
│ demba_allen_seg_dev_mouse_p53_2… 1.0 │
│ demba_allen_seg_dev_mouse_p54_2… 1.0 │
│ demba_allen_seg_dev_mouse_p54_2… 1.0 │
│ demba_allen_seg_dev_mouse_p55_2… 1.0 │
│ demba_allen_seg_dev_mouse_p55_2… 1.0 │
│ demba_allen_seg_dev_mouse_p56_2… 1.0 │
│ demba_allen_seg_dev_mouse_p56_2… 1.0 │
│ demba_allen_seg_dev_mouse_p5_20… 1.0 │
│ demba_allen_seg_dev_mouse_p5_25… 1.0 │
│ demba_allen_seg_dev_mouse_p6_20… 1.0 │
│ demba_allen_seg_dev_mouse_p6_25… 1.0 │
│ demba_allen_seg_dev_mouse_p7_20… 1.0 │
│ demba_allen_seg_dev_mouse_p7_25… 1.0 │
│ demba_allen_seg_dev_mouse_p8_20… 1.0 │
│ demba_allen_seg_dev_mouse_p8_25… 1.0 │
│ demba_allen_seg_dev_mouse_p9_20… 1.0 │
│ demba_allen_seg_dev_mouse_p9_25… 1.0 │
│ dorr_mouse_mri_32um 1.0 │
│ drosophila_wingdisc_instar3_2um 1.0 │
│ eurasian_blackcap_25um 1.5 │
│ example_mouse_100um 1.2 │
│ kim_dev_mouse_e11-5_lsfm_20um 1.3 │
│ kim_dev_mouse_e11-5_mri-adc_31.… 1.3 │
│ kim_dev_mouse_e11-5_mri-dwi_31.… 1.3 │
│ kim_dev_mouse_e11-5_mri-fa_31.5… 1.3 │
│ kim_dev_mouse_e11-5_mri-t2_31.5… 1.3 │
│ kim_dev_mouse_e13-5_lsfm_20um 1.3 │
│ kim_dev_mouse_e13-5_mri-adc_34um 1.3 │
│ kim_dev_mouse_e13-5_mri-dwi_34um 1.3 │
│ kim_dev_mouse_e13-5_mri-fa_34um 1.3 │
│ kim_dev_mouse_e13-5_mri-t2_34um 1.3 │
│ kim_dev_mouse_e15-5_lsfm_20um 1.3 │
│ kim_dev_mouse_e15-5_mri-adc_37.… 1.3 │
│ kim_dev_mouse_e15-5_mri-dwi_37.… 1.3 │
│ kim_dev_mouse_e15-5_mri-fa_37.5… 1.3 │
│ kim_dev_mouse_e15-5_mri-mtr_37.… 1.3 │
│ kim_dev_mouse_e15-5_mri-t2_37.5… 1.3 │
│ kim_dev_mouse_e18-5_lsfm_20um 1.3 │
│ kim_dev_mouse_e18-5_mri-adc_40um 1.3 │
│ kim_dev_mouse_e18-5_mri-dwi_40um 1.3 │
│ kim_dev_mouse_e18-5_mri-fa_40um 1.3 │
│ kim_dev_mouse_e18-5_mri-t2_40um 1.3 │
│ kim_dev_mouse_idisco_10um 1.2 │
│ kim_dev_mouse_mri_a0_10um 1.2 │
│ kim_dev_mouse_mri_adc_10um 1.2 │
│ kim_dev_mouse_mri_dwi_10um 1.2 │
│ kim_dev_mouse_mri_fa_10um 1.2 │
│ kim_dev_mouse_mri_mtr_10um 1.2 │
│ kim_dev_mouse_mri_t2_10um 1.2 │
│ kim_dev_mouse_p04_lsfm_20um 1.3 │
│ kim_dev_mouse_p04_mri-adc_50um 1.3 │
│ kim_dev_mouse_p04_mri-dwi_50um 1.3 │
│ kim_dev_mouse_p04_mri-fa_50um 1.3 │
│ kim_dev_mouse_p04_mri-mtr_50um 1.3 │
│ kim_dev_mouse_p04_mri-t2_50um 1.3 │
│ kim_dev_mouse_p14_lsfm_20um 1.3 │
│ kim_dev_mouse_p14_mri-adc_50um 1.3 │
│ kim_dev_mouse_p14_mri-dwi_50um 1.3 │
│ kim_dev_mouse_p14_mri-fa_50um 1.3 │
│ kim_dev_mouse_p14_mri-mtr_50um 1.3 │
│ kim_dev_mouse_p14_mri-t2_50um 1.3 │
│ kim_dev_mouse_p56_lsfm_20um 1.3 │
│ kim_dev_mouse_p56_mri-adc_50um 1.3 │
│ kim_dev_mouse_p56_mri-dwi_50um 1.3 │
│ kim_dev_mouse_p56_mri-fa_50um 1.3 │
│ kim_dev_mouse_p56_mri-t2_50um 1.3 │
│ kim_dev_mouse_stp_10um 1.2 │
│ kim_mouse_100um 1.1 │
│ kim_mouse_10um 1.1 │
│ kim_mouse_25um 1.1 │
│ kim_mouse_50um 1.1 │
│ kim_mouse_isotropic_20um 1.0 │
│ kocher_bumblebee_2.542um 1.0 │
│ mpin_zfish_1um 1.0 │
│ nadkarni_mri_mouselemur_91um 1.1 │
│ osten_mouse_100um 1.1 │
│ osten_mouse_10um 1.1 │
│ osten_mouse_25um 1.1 │
│ osten_mouse_50um 1.1 │
│ perens_lsfm_mouse_20um 1.2 │
│ perens_multimodal_lsfm_25um 1.0 │
│ perens_stereotaxic_mri_mouse_25… 1.0 │
│ prairie_vole_25um 1.0 │
│ princeton_mouse_20um 1.1 │
│ sju_cavefish_2um 1.0 │
│ swc_female_rat_50um 1.0 │
│ unam_axolotl_40um 1.1 │
│ whs_sd_rat_39um 1.2 │
│ whs_sd_swc_female_rat_39um 1.0 │
╰──────────────────────────────────────────────────────────────────────────────╯
Creating a BrainGlobeAtlas object#
To instantiate a BrainGlobeAtlas object, we call it with the atlas name. The first time we use it, the latest version of the atlas files will be downloaded from the remote GIN repository and stored on your local machine (by default, in ~/.brainglobe):
atlas = BrainGlobeAtlas("allen_mouse_100um", check_latest=False)
Downloading... ━━━━━━━━━━ 100.0% • 61.0/61.0 • speed: 19.7 MB/s • ETA: 0:00:00
MB
Atlas quality
Usually BrainGlobe only packages existing atlases. The quality of the underlying images and atlas ontology relies on the original atlas data, and this can vary considerably. In this example, we choose the “allen_mouse_100um” atlas, as it is relatively small, but high quality.
Using the atlas#
A BrainGlobe atlas is a convenient API for interacting with an anatomical atlas. BrainGlobe atlases contain:
Metadata
Reference anatomical stack
Region annotation stack
Hemisphere annotation stack
Description of the region hierarchy
Meshes for the regions
Metadata#
All atlases have a standard set of metatata describing their source, species, resolution, etc:
metadata = atlas.metadata
pprint(metadata)
{'additional_references': [],
'atlas_link': 'http://www.brain-map.org',
'citation': 'Wang et al 2020, https://doi.org/10.1016/j.cell.2020.04.007',
'name': 'allen_mouse',
'orientation': 'asr',
'resolution': [100.0, 100.0, 100.0],
'shape': [132, 80, 114],
'species': 'Mus musculus',
'symmetric': True,
'trasform_to_bg': [[1.0, 0.0, 0.0, 0.0],
[0.0, 1.0, 0.0, 0.0],
[0.0, 0.0, 1.0, 0.0],
[0.0, 0.0, 0.0, 1.0]],
'version': '1.2'}
Anatomical, annotation and hemispheres stacks#
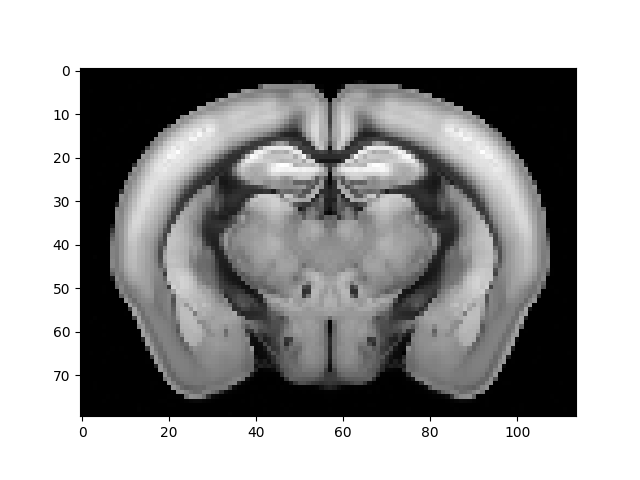
Anatomical reference (or template) image:
reference = atlas.reference
# Get the middle section and plot
middle_section = reference.shape[0] // 2
plt.imshow(reference[middle_section,:,:], cmap='gray')
<matplotlib.image.AxesImage object at 0x7f923d8463c0>
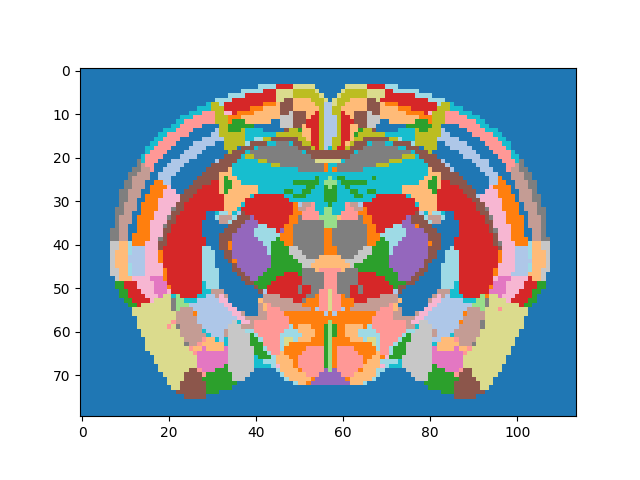
Annotations stack
annotation = atlas.annotation
# Create a cyclic colormap due to the high values in the Allen atlas
N = 512
colors = cm.get_cmap('tab20').resampled(N)
lut = colors(np.arange(N))
# Map label image to lookup table and plot
plt.imshow(lut[annotation[middle_section,:,:] % N])
<matplotlib.image.AxesImage object at 0x7f923d5d3560>
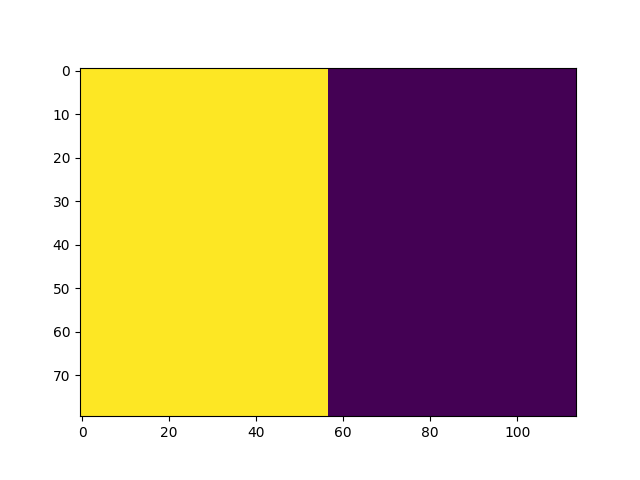
Hemisheres stack:
hemispheres = atlas.hemispheres
plt.imshow(hemispheres[middle_section,:,:])
<matplotlib.image.AxesImage object at 0x7f923d6b80e0>
Regions hierarchy#
The atlas comes with the description of a hierarchy of brain structures. To see an overview:
print(atlas.structures)
root (997)
├── VS (73)
│ ├── AQ (140)
│ ├── V3 (129)
│ ├── V4 (145)
│ │ └── V4r (153)
│ ├── VL (81)
│ │ ├── SEZ (98)
│ │ └── chpl (108)
│ └── c (164)
├── fiber tracts (1009)
│ ├── cbf (960)
│ │ ├── arb (728)
│ │ ├── cbc (744)
│ │ └── cbp (752)
│ │ ├── icp (1123)
│ │ │ └── sctd (553)
│ │ ├── mcp (78)
│ │ └── scp (326)
│ │ ├── dscp (812)
│ │ ├── sctv (866)
│ │ └── uf (850)
│ ├── cm (967)
│ │ ├── IIIn (832)
│ │ │ ├── mlf (62)
│ │ │ └── pc (158)
│ │ ├── IIn (848)
│ │ │ ├── bsc (916)
│ │ │ ├── csc (336)
│ │ │ ├── och (117)
│ │ │ └── opt (125)
│ │ ├── IVn (911)
│ │ ├── In (840)
│ │ │ ├── aco (900)
│ │ │ ├── lotg (21)
│ │ │ │ ├── lot (665)
│ │ │ │ └── lotd (538)
│ │ │ └── onl (1016)
│ │ ├── VIIIn (933)
│ │ │ ├── cVIIIn (948)
│ │ │ │ ├── bic (482)
│ │ │ │ ├── cic (633)
│ │ │ │ ├── das (506)
│ │ │ │ ├── ll (658)
│ │ │ │ └── tb (841)
│ │ │ └── vVIIIn (413)
│ │ ├── VIIn (798)
│ │ │ └── gVIIn (1116)
│ │ ├── Vn (901)
│ │ │ ├── moV (93)
│ │ │ └── sV (229)
│ │ │ └── sptV (794)
│ │ ├── Xn (917)
│ │ │ └── ts (237)
│ │ ├── drt (792)
│ │ │ └── cett (932)
│ │ │ ├── dc (514)
│ │ │ │ └── cuf (380)
│ │ │ └── ml (697)
│ │ └── von (949)
│ ├── eps (1000)
│ │ ├── epsc (760)
│ │ │ └── nst (102)
│ │ ├── rust (863)
│ │ │ └── vtd (397)
│ │ └── tsp (877)
│ │ ├── dtd (1060)
│ │ ├── tspc (1043)
│ │ └── tspd (1051)
│ ├── lfbs (983)
│ │ ├── cc (776)
│ │ │ ├── ccb (484682516)
│ │ │ ├── ccg (1108)
│ │ │ ├── ccs (986)
│ │ │ ├── ee (964)
│ │ │ ├── fa (956)
│ │ │ │ └── ec (579)
│ │ │ └── fp (971)
│ │ ├── cst (784)
│ │ │ ├── cpd (924)
│ │ │ ├── int (6)
│ │ │ ├── py (190)
│ │ │ └── pyd (198)
│ │ └── lfbst (896)
│ │ ├── ar (484682524)
│ │ ├── em (1092)
│ │ └── or (484682520)
│ ├── mfbs (991)
│ │ ├── mfbc (768)
│ │ │ ├── act (908)
│ │ │ ├── amc (884)
│ │ │ ├── cing (940)
│ │ │ ├── fxs (1099)
│ │ │ │ ├── alv (466)
│ │ │ │ ├── df (530)
│ │ │ │ ├── fi (603)
│ │ │ │ ├── fxpo (737)
│ │ │ │ │ ├── fx (436)
│ │ │ │ │ └── mct (428)
│ │ │ │ └── hc (618)
│ │ │ │ ├── dhc (443)
│ │ │ │ └── vhc (449)
│ │ │ └── st (301)
│ │ │ └── stc (484682528)
│ │ └── mfsbshy (824)
│ │ ├── mfb (54)
│ │ ├── mfbse (1083)
│ │ │ ├── fr (595)
│ │ │ ├── hbc (611)
│ │ │ └── sm (802)
│ │ ├── mfbsma (46)
│ │ │ ├── mp (673)
│ │ │ ├── mtg (681)
│ │ │ ├── mtt (690)
│ │ │ └── pm (753)
│ │ └── sup (349)
│ └── scwm (484682512)
└── grey (8)
├── BS (343)
│ ├── HB (1065)
│ │ ├── MY (354)
│ │ │ ├── MY-mot (370)
│ │ │ │ ├── ACVII (576)
│ │ │ │ ├── AMB (135)
│ │ │ │ │ ├── AMBd (939)
│ │ │ │ │ └── AMBv (143)
│ │ │ │ ├── DMX (839)
│ │ │ │ ├── GRN (1048)
│ │ │ │ ├── ICB (372)
│ │ │ │ ├── IO (83)
│ │ │ │ ├── IRN (136)
│ │ │ │ ├── ISN (106)
│ │ │ │ ├── LIN (203)
│ │ │ │ ├── LRN (235)
│ │ │ │ │ ├── LRNm (955)
│ │ │ │ │ └── LRNp (963)
│ │ │ │ ├── MARN (307)
│ │ │ │ ├── MDRN (395)
│ │ │ │ │ ├── MDRNd (1098)
│ │ │ │ │ └── MDRNv (1107)
│ │ │ │ ├── PARN (852)
│ │ │ │ ├── PAS (859)
│ │ │ │ ├── PGRN (938)
│ │ │ │ │ ├── PGRNd (970)
│ │ │ │ │ └── PGRNl (978)
│ │ │ │ ├── PHY (154)
│ │ │ │ │ ├── NR (177)
│ │ │ │ │ └── PRP (169)
│ │ │ │ ├── PPY (1069)
│ │ │ │ ├── VI (653)
│ │ │ │ ├── VII (661)
│ │ │ │ ├── VNC (701)
│ │ │ │ │ ├── LAV (209)
│ │ │ │ │ ├── MV (202)
│ │ │ │ │ ├── SPIV (225)
│ │ │ │ │ └── SUV (217)
│ │ │ │ ├── XII (773)
│ │ │ │ ├── x (765)
│ │ │ │ └── y (781)
│ │ │ ├── MY-sat (379)
│ │ │ │ ├── RM (206)
│ │ │ │ ├── RO (222)
│ │ │ │ └── RPA (230)
│ │ │ └── MY-sen (386)
│ │ │ ├── AP (207)
│ │ │ ├── CN (607)
│ │ │ │ ├── DCO (96)
│ │ │ │ └── VCO (101)
│ │ │ ├── DCN (720)
│ │ │ │ ├── CU (711)
│ │ │ │ └── GR (1039)
│ │ │ ├── ECU (903)
│ │ │ ├── NTB (642)
│ │ │ ├── NTS (651)
│ │ │ ├── Pa5 (589508451)
│ │ │ ├── SPVC (429)
│ │ │ ├── SPVI (437)
│ │ │ └── SPVO (445)
│ │ └── P (771)
│ │ ├── P-mot (987)
│ │ │ ├── Acs5 (549009219)
│ │ │ ├── B (280)
│ │ │ ├── DTN (880)
│ │ │ ├── I5 (549009227)
│ │ │ ├── P5 (549009215)
│ │ │ ├── PC5 (549009223)
│ │ │ ├── PCG (898)
│ │ │ ├── PDTg (599626927)
│ │ │ ├── PG (931)
│ │ │ ├── PRNc (1093)
│ │ │ ├── SG (318)
│ │ │ ├── SUT (534)
│ │ │ ├── TRN (574)
│ │ │ └── V (621)
│ │ ├── P-sat (1117)
│ │ │ ├── CS (679)
│ │ │ ├── LC (147)
│ │ │ ├── LDT (162)
│ │ │ ├── NI (604)
│ │ │ ├── PRNr (146)
│ │ │ ├── RPO (238)
│ │ │ ├── SLC (350)
│ │ │ └── SLD (358)
│ │ └── P-sen (1132)
│ │ ├── NLL (612)
│ │ ├── PB (867)
│ │ │ └── KF (123)
│ │ ├── PSV (7)
│ │ └── SOC (398)
│ │ ├── POR (122)
│ │ ├── SOCl (114)
│ │ └── SOCm (105)
│ ├── IB (1129)
│ │ ├── HY (1097)
│ │ │ ├── LZ (290)
│ │ │ │ ├── LHA (194)
│ │ │ │ ├── LPO (226)
│ │ │ │ ├── PST (356)
│ │ │ │ ├── PSTN (364)
│ │ │ │ ├── PeF (576073704)
│ │ │ │ ├── RCH (173)
│ │ │ │ ├── STN (470)
│ │ │ │ ├── TU (614)
│ │ │ │ └── ZI (797)
│ │ │ │ └── FF (804)
│ │ │ ├── ME (10671)
│ │ │ ├── MEZ (467)
│ │ │ │ ├── AHN (88)
│ │ │ │ ├── MBO (331)
│ │ │ │ │ ├── LM (210)
│ │ │ │ │ ├── MM (491)
│ │ │ │ │ │ ├── MMd (606826659)
│ │ │ │ │ │ ├── MMl (606826647)
│ │ │ │ │ │ ├── MMm (606826651)
│ │ │ │ │ │ ├── MMme (732)
│ │ │ │ │ │ └── MMp (606826655)
│ │ │ │ │ ├── SUM (525)
│ │ │ │ │ └── TM (557)
│ │ │ │ │ ├── TMd (1126)
│ │ │ │ │ └── TMv (1)
│ │ │ │ ├── MPN (515)
│ │ │ │ ├── PH (946)
│ │ │ │ ├── PMd (980)
│ │ │ │ ├── PMv (1004)
│ │ │ │ ├── PVHd (63)
│ │ │ │ └── VMH (693)
│ │ │ ├── PVR (141)
│ │ │ │ ├── ADP (72)
│ │ │ │ ├── AVP (263)
│ │ │ │ ├── AVPV (272)
│ │ │ │ ├── DMH (830)
│ │ │ │ ├── MEPO (452)
│ │ │ │ ├── MPO (523)
│ │ │ │ ├── OV (763)
│ │ │ │ ├── PD (914)
│ │ │ │ ├── PS (1109)
│ │ │ │ ├── PVp (126)
│ │ │ │ ├── PVpo (133)
│ │ │ │ ├── SBPV (347)
│ │ │ │ ├── SCH (286)
│ │ │ │ ├── SFO (338)
│ │ │ │ ├── VLPO (689)
│ │ │ │ └── VMPO (576073699)
│ │ │ └── PVZ (157)
│ │ │ ├── ARH (223)
│ │ │ ├── ASO (332)
│ │ │ ├── PVH (38)
│ │ │ ├── PVa (30)
│ │ │ ├── PVi (118)
│ │ │ └── SO (390)
│ │ └── TH (549)
│ │ ├── DORpm (856)
│ │ │ ├── ATN (239)
│ │ │ │ ├── AD (64)
│ │ │ │ ├── AM (127)
│ │ │ │ │ ├── AMd (1096)
│ │ │ │ │ └── AMv (1104)
│ │ │ │ ├── AV (255)
│ │ │ │ ├── IAD (1113)
│ │ │ │ ├── IAM (1120)
│ │ │ │ └── LD (155)
│ │ │ ├── EPI (958)
│ │ │ │ ├── LH (186)
│ │ │ │ └── MH (483)
│ │ │ ├── GENv (1014)
│ │ │ │ ├── IGL (27)
│ │ │ │ ├── IntG (563807439)
│ │ │ │ ├── LGv (178)
│ │ │ │ └── SubG (321)
│ │ │ ├── ILM (51)
│ │ │ │ ├── CL (575)
│ │ │ │ ├── CM (599)
│ │ │ │ ├── PCN (907)
│ │ │ │ ├── PF (930)
│ │ │ │ ├── PIL (560581563)
│ │ │ │ └── RH (189)
│ │ │ ├── LAT (138)
│ │ │ │ ├── Eth (560581551)
│ │ │ │ ├── LP (218)
│ │ │ │ ├── PO (1020)
│ │ │ │ ├── POL (1029)
│ │ │ │ └── SGN (325)
│ │ │ ├── MED (444)
│ │ │ │ ├── IMD (59)
│ │ │ │ ├── MD (362)
│ │ │ │ ├── PR (1077)
│ │ │ │ └── SMT (366)
│ │ │ ├── MTN (571)
│ │ │ │ ├── PT (15)
│ │ │ │ ├── PVT (149)
│ │ │ │ ├── RE (181)
│ │ │ │ └── Xi (560581559)
│ │ │ └── RT (262)
│ │ └── DORsm (864)
│ │ ├── GENd (1008)
│ │ │ ├── LGd (170)
│ │ │ │ ├── LGd-co (496345668)
│ │ │ │ ├── LGd-ip (496345672)
│ │ │ │ └── LGd-sh (496345664)
│ │ │ └── MG (475)
│ │ │ ├── MGd (1072)
│ │ │ ├── MGm (1088)
│ │ │ └── MGv (1079)
│ │ ├── PP (1044)
│ │ ├── SPA (609)
│ │ ├── SPF (406)
│ │ │ ├── SPFm (414)
│ │ │ └── SPFp (422)
│ │ └── VENT (637)
│ │ ├── PoT (563807435)
│ │ ├── VAL (629)
│ │ ├── VM (685)
│ │ └── VP (709)
│ │ ├── VPL (718)
│ │ ├── VPLpc (725)
│ │ ├── VPM (733)
│ │ └── VPMpc (741)
│ └── MB (313)
│ ├── MBmot (323)
│ │ ├── AT (231)
│ │ ├── CUN (616)
│ │ ├── DT (75)
│ │ ├── EW (975)
│ │ ├── III (35)
│ │ ├── IV (115)
│ │ ├── LT (66)
│ │ ├── MA3 (549009211)
│ │ ├── MRN (128)
│ │ ├── MT (58)
│ │ ├── PAG (795)
│ │ │ ├── INC (67)
│ │ │ ├── ND (587)
│ │ │ ├── PRC (50)
│ │ │ └── Su3 (614454277)
│ │ ├── PN (607344830)
│ │ ├── PRT (1100)
│ │ │ ├── APN (215)
│ │ │ ├── MPT (531)
│ │ │ ├── NOT (628)
│ │ │ ├── NPC (634)
│ │ │ ├── OP (706)
│ │ │ ├── PPT (1061)
│ │ │ └── RPF (549009203)
│ │ ├── Pa4 (606826663)
│ │ ├── RN (214)
│ │ ├── RR (246)
│ │ ├── SCm (294)
│ │ │ ├── SCdg (26)
│ │ │ ├── SCdw (42)
│ │ │ ├── SCig (10)
│ │ │ └── SCiw (17)
│ │ ├── SNr (381)
│ │ ├── VTA (749)
│ │ └── VTN (757)
│ ├── MBsen (339)
│ │ ├── IC (4)
│ │ │ ├── ICc (811)
│ │ │ ├── ICd (820)
│ │ │ └── ICe (828)
│ │ ├── MEV (460)
│ │ ├── NB (580)
│ │ ├── PBG (874)
│ │ ├── SAG (271)
│ │ ├── SCO (599626923)
│ │ └── SCs (302)
│ │ ├── SCop (851)
│ │ ├── SCsg (842)
│ │ └── SCzo (834)
│ └── MBsta (348)
│ ├── PPN (1052)
│ ├── RAmb (165)
│ │ ├── CLI (591)
│ │ ├── DR (872)
│ │ ├── IF (12)
│ │ ├── IPN (100)
│ │ │ ├── IPA (607344842)
│ │ │ ├── IPC (607344838)
│ │ │ ├── IPDL (607344858)
│ │ │ ├── IPDM (607344854)
│ │ │ ├── IPI (607344850)
│ │ │ ├── IPL (607344846)
│ │ │ ├── IPR (607344834)
│ │ │ └── IPRL (607344862)
│ │ └── RL (197)
│ └── SNc (374)
├── CB (512)
│ ├── CBN (519)
│ │ ├── DN (846)
│ │ ├── FN (989)
│ │ ├── IP (91)
│ │ └── VeCB (589508455)
│ └── CBX (528)
│ ├── HEM (1073)
│ │ ├── AN (1017)
│ │ │ ├── ANcr1 (1056)
│ │ │ └── ANcr2 (1064)
│ │ ├── COPY (1033)
│ │ ├── FL (1049)
│ │ ├── PFL (1041)
│ │ ├── PRM (1025)
│ │ └── SIM (1007)
│ └── VERM (645)
│ ├── CENT (920)
│ │ ├── CENT2 (976)
│ │ └── CENT3 (984)
│ ├── CUL (928)
│ │ └── CUL4, 5 (1091)
│ ├── DEC (936)
│ ├── FOTU (944)
│ ├── LING (912)
│ ├── NOD (968)
│ ├── PYR (951)
│ └── UVU (957)
└── CH (567)
├── CNU (623)
│ ├── PAL (803)
│ │ ├── PALc (809)
│ │ │ ├── BAC (287)
│ │ │ └── BST (351)
│ │ ├── PALd (818)
│ │ │ ├── GPe (1022)
│ │ │ └── GPi (1031)
│ │ ├── PALm (826)
│ │ │ ├── MSC (904)
│ │ │ │ ├── MS (564)
│ │ │ │ └── NDB (596)
│ │ │ └── TRS (581)
│ │ └── PALv (835)
│ │ ├── MA (298)
│ │ └── SI (342)
│ └── STR (477)
│ ├── LSX (275)
│ │ ├── LS (242)
│ │ │ ├── LSc (250)
│ │ │ ├── LSr (258)
│ │ │ └── LSv (266)
│ │ ├── SF (310)
│ │ └── SH (333)
│ ├── STRd (485)
│ │ └── CP (672)
│ ├── STRv (493)
│ │ ├── ACB (56)
│ │ ├── FS (998)
│ │ └── OT (754)
│ └── sAMY (278)
│ ├── AAA (23)
│ ├── BA (292)
│ ├── CEA (536)
│ │ ├── CEAc (544)
│ │ ├── CEAl (551)
│ │ └── CEAm (559)
│ ├── IA (1105)
│ └── MEA (403)
└── CTX (688)
├── CTXpl (695)
│ ├── HPF (1089)
│ │ ├── HIP (1080)
│ │ │ ├── CA (375)
│ │ │ │ ├── CA1 (382)
│ │ │ │ ├── CA2 (423)
│ │ │ │ └── CA3 (463)
│ │ │ ├── DG (726)
│ │ │ │ ├── DG-mo (10703)
│ │ │ │ ├── DG-po (10704)
│ │ │ │ └── DG-sg (632)
│ │ │ ├── FC (982)
│ │ │ └── IG (19)
│ │ └── RHP (822)
│ │ ├── APr (484682508)
│ │ ├── ENT (909)
│ │ │ ├── ENTl (918)
│ │ │ │ ├── ENTl1 (1121)
│ │ │ │ ├── ENTl2 (20)
│ │ │ │ ├── ENTl3 (52)
│ │ │ │ ├── ENTl5 (139)
│ │ │ │ └── ENTl6a (28)
│ │ │ └── ENTm (926)
│ │ │ ├── ENTm1 (526)
│ │ │ ├── ENTm2 (543)
│ │ │ ├── ENTm3 (664)
│ │ │ ├── ENTm5 (727)
│ │ │ └── ENTm6 (743)
│ │ ├── HATA (589508447)
│ │ ├── PAR (843)
│ │ ├── POST (1037)
│ │ ├── PRE (1084)
│ │ ├── ProS (484682470)
│ │ └── SUB (502)
│ ├── Isocortex (315)
│ │ ├── ACA (31)
│ │ │ ├── ACAd (39)
│ │ │ │ ├── ACAd1 (935)
│ │ │ │ ├── ACAd2/3 (211)
│ │ │ │ ├── ACAd5 (1015)
│ │ │ │ ├── ACAd6a (919)
│ │ │ │ └── ACAd6b (927)
│ │ │ └── ACAv (48)
│ │ │ ├── ACAv1 (588)
│ │ │ ├── ACAv2/3 (296)
│ │ │ ├── ACAv5 (772)
│ │ │ ├── ACAv6a (810)
│ │ │ └── ACAv6b (819)
│ │ ├── AI (95)
│ │ │ ├── AId (104)
│ │ │ │ ├── AId1 (996)
│ │ │ │ ├── AId2/3 (328)
│ │ │ │ ├── AId5 (1101)
│ │ │ │ ├── AId6a (783)
│ │ │ │ └── AId6b (831)
│ │ │ ├── AIp (111)
│ │ │ │ ├── AIp1 (120)
│ │ │ │ ├── AIp2/3 (163)
│ │ │ │ ├── AIp5 (344)
│ │ │ │ ├── AIp6a (314)
│ │ │ │ └── AIp6b (355)
│ │ │ └── AIv (119)
│ │ │ ├── AIv1 (704)
│ │ │ ├── AIv2/3 (694)
│ │ │ ├── AIv5 (800)
│ │ │ ├── AIv6a (675)
│ │ │ └── AIv6b (699)
│ │ ├── AUD (247)
│ │ │ ├── AUDd (1011)
│ │ │ │ ├── AUDd1 (527)
│ │ │ │ ├── AUDd2/3 (600)
│ │ │ │ ├── AUDd4 (678)
│ │ │ │ ├── AUDd5 (252)
│ │ │ │ ├── AUDd6a (156)
│ │ │ │ └── AUDd6b (243)
│ │ │ ├── AUDp (1002)
│ │ │ │ ├── AUDp1 (735)
│ │ │ │ ├── AUDp2/3 (251)
│ │ │ │ ├── AUDp4 (816)
│ │ │ │ ├── AUDp5 (847)
│ │ │ │ ├── AUDp6a (954)
│ │ │ │ └── AUDp6b (1005)
│ │ │ ├── AUDpo (1027)
│ │ │ │ ├── AUDpo1 (696)
│ │ │ │ ├── AUDpo2/3 (643)
│ │ │ │ ├── AUDpo4 (759)
│ │ │ │ ├── AUDpo5 (791)
│ │ │ │ ├── AUDpo6a (249)
│ │ │ │ └── AUDpo6b (456)
│ │ │ └── AUDv (1018)
│ │ │ ├── AUDv1 (959)
│ │ │ ├── AUDv2/3 (755)
│ │ │ ├── AUDv4 (990)
│ │ │ ├── AUDv5 (1023)
│ │ │ ├── AUDv6a (520)
│ │ │ └── AUDv6b (598)
│ │ ├── ECT (895)
│ │ │ ├── ECT1 (836)
│ │ │ ├── ECT2/3 (427)
│ │ │ ├── ECT5 (988)
│ │ │ ├── ECT6a (977)
│ │ │ └── ECT6b (1045)
│ │ ├── FRP (184)
│ │ │ ├── FRP1 (68)
│ │ │ ├── FRP2/3 (667)
│ │ │ ├── FRP5 (526157192)
│ │ │ ├── FRP6a (526157196)
│ │ │ └── FRP6b (526322264)
│ │ ├── GU (1057)
│ │ │ ├── GU1 (36)
│ │ │ ├── GU2/3 (180)
│ │ │ ├── GU4 (148)
│ │ │ ├── GU5 (187)
│ │ │ ├── GU6a (638)
│ │ │ └── GU6b (662)
│ │ ├── ILA (44)
│ │ │ ├── ILA1 (707)
│ │ │ ├── ILA2/3 (556)
│ │ │ ├── ILA5 (827)
│ │ │ ├── ILA6a (1054)
│ │ │ └── ILA6b (1081)
│ │ ├── MO (500)
│ │ │ ├── MOp (985)
│ │ │ │ ├── MOp1 (320)
│ │ │ │ ├── MOp2/3 (943)
│ │ │ │ ├── MOp5 (648)
│ │ │ │ ├── MOp6a (844)
│ │ │ │ └── MOp6b (882)
│ │ │ └── MOs (993)
│ │ │ ├── MOs1 (656)
│ │ │ ├── MOs2/3 (962)
│ │ │ ├── MOs5 (767)
│ │ │ ├── MOs6a (1021)
│ │ │ └── MOs6b (1085)
│ │ ├── ORB (714)
│ │ │ ├── ORBl (723)
│ │ │ │ ├── ORBl1 (448)
│ │ │ │ ├── ORBl2/3 (412)
│ │ │ │ ├── ORBl5 (630)
│ │ │ │ ├── ORBl6a (440)
│ │ │ │ └── ORBl6b (488)
│ │ │ ├── ORBm (731)
│ │ │ │ ├── ORBm1 (484)
│ │ │ │ ├── ORBm2/3 (582)
│ │ │ │ ├── ORBm5 (620)
│ │ │ │ ├── ORBm6a (910)
│ │ │ │ └── ORBm6b (527696977)
│ │ │ └── ORBvl (746)
│ │ │ ├── ORBvl1 (969)
│ │ │ ├── ORBvl2/3 (288)
│ │ │ ├── ORBvl5 (1125)
│ │ │ ├── ORBvl6a (608)
│ │ │ └── ORBvl6b (680)
│ │ ├── PERI (922)
│ │ │ ├── PERI1 (540)
│ │ │ ├── PERI2/3 (888)
│ │ │ ├── PERI5 (692)
│ │ │ ├── PERI6a (335)
│ │ │ └── PERI6b (368)
│ │ ├── PL (972)
│ │ │ ├── PL1 (171)
│ │ │ ├── PL2/3 (304)
│ │ │ ├── PL5 (363)
│ │ │ ├── PL6a (84)
│ │ │ └── PL6b (132)
│ │ ├── PTLp (22)
│ │ │ ├── VISa (312782546)
│ │ │ │ ├── VISa1 (312782550)
│ │ │ │ ├── VISa2/3 (312782554)
│ │ │ │ ├── VISa4 (312782558)
│ │ │ │ ├── VISa5 (312782562)
│ │ │ │ ├── VISa6a (312782566)
│ │ │ │ └── VISa6b (312782570)
│ │ │ └── VISrl (417)
│ │ │ ├── VISrl1 (312782604)
│ │ │ ├── VISrl2/3 (312782608)
│ │ │ ├── VISrl4 (312782612)
│ │ │ ├── VISrl5 (312782616)
│ │ │ ├── VISrl6a (312782620)
│ │ │ └── VISrl6b (312782624)
│ │ ├── RSP (254)
│ │ │ ├── RSPagl (894)
│ │ │ │ ├── RSPagl1 (671)
│ │ │ │ ├── RSPagl2/3 (965)
│ │ │ │ ├── RSPagl5 (774)
│ │ │ │ ├── RSPagl6a (906)
│ │ │ │ └── RSPagl6b (279)
│ │ │ ├── RSPd (879)
│ │ │ │ ├── RSPd1 (442)
│ │ │ │ ├── RSPd2/3 (434)
│ │ │ │ ├── RSPd4 (545)
│ │ │ │ ├── RSPd5 (610)
│ │ │ │ ├── RSPd6a (274)
│ │ │ │ └── RSPd6b (330)
│ │ │ └── RSPv (886)
│ │ │ ├── RSPv1 (542)
│ │ │ ├── RSPv2/3 (430)
│ │ │ ├── RSPv5 (687)
│ │ │ ├── RSPv6a (590)
│ │ │ └── RSPv6b (622)
│ │ ├── SS (453)
│ │ │ ├── SSp (322)
│ │ │ │ ├── SSp-bfd (329)
│ │ │ │ │ ├── SSp-bfd1 (981)
│ │ │ │ │ ├── SSp-bfd2/3 (201)
│ │ │ │ │ ├── SSp-bfd4 (1047)
│ │ │ │ │ ├── SSp-bfd5 (1070)
│ │ │ │ │ ├── SSp-bfd6a (1038)
│ │ │ │ │ └── SSp-bfd6b (1062)
│ │ │ │ ├── SSp-ll (337)
│ │ │ │ │ ├── SSp-ll1 (1030)
│ │ │ │ │ ├── SSp-ll2/3 (113)
│ │ │ │ │ ├── SSp-ll4 (1094)
│ │ │ │ │ ├── SSp-ll5 (1128)
│ │ │ │ │ ├── SSp-ll6a (478)
│ │ │ │ │ └── SSp-ll6b (510)
│ │ │ │ ├── SSp-m (345)
│ │ │ │ │ ├── SSp-m1 (878)
│ │ │ │ │ ├── SSp-m2/3 (657)
│ │ │ │ │ ├── SSp-m4 (950)
│ │ │ │ │ ├── SSp-m5 (974)
│ │ │ │ │ ├── SSp-m6a (1102)
│ │ │ │ │ └── SSp-m6b (2)
│ │ │ │ ├── SSp-n (353)
│ │ │ │ │ ├── SSp-n1 (558)
│ │ │ │ │ ├── SSp-n2/3 (838)
│ │ │ │ │ ├── SSp-n4 (654)
│ │ │ │ │ ├── SSp-n5 (702)
│ │ │ │ │ ├── SSp-n6a (889)
│ │ │ │ │ └── SSp-n6b (929)
│ │ │ │ ├── SSp-tr (361)
│ │ │ │ │ ├── SSp-tr1 (1006)
│ │ │ │ │ ├── SSp-tr2/3 (670)
│ │ │ │ │ ├── SSp-tr4 (1086)
│ │ │ │ │ ├── SSp-tr5 (1111)
│ │ │ │ │ ├── SSp-tr6a (9)
│ │ │ │ │ └── SSp-tr6b (461)
│ │ │ │ ├── SSp-ul (369)
│ │ │ │ │ ├── SSp-ul1 (450)
│ │ │ │ │ ├── SSp-ul2/3 (854)
│ │ │ │ │ ├── SSp-ul4 (577)
│ │ │ │ │ ├── SSp-ul5 (625)
│ │ │ │ │ ├── SSp-ul6a (945)
│ │ │ │ │ └── SSp-ul6b (1026)
│ │ │ │ └── SSp-un (182305689)
│ │ │ │ ├── SSp-un1 (182305693)
│ │ │ │ ├── SSp-un2/3 (182305697)
│ │ │ │ ├── SSp-un4 (182305701)
│ │ │ │ ├── SSp-un5 (182305705)
│ │ │ │ ├── SSp-un6a (182305709)
│ │ │ │ └── SSp-un6b (182305713)
│ │ │ └── SSs (378)
│ │ │ ├── SSs1 (873)
│ │ │ ├── SSs2/3 (806)
│ │ │ ├── SSs4 (1035)
│ │ │ ├── SSs5 (1090)
│ │ │ ├── SSs6a (862)
│ │ │ └── SSs6b (893)
│ │ ├── TEa (541)
│ │ │ ├── TEa1 (97)
│ │ │ ├── TEa2/3 (1127)
│ │ │ ├── TEa4 (234)
│ │ │ ├── TEa5 (289)
│ │ │ ├── TEa6a (729)
│ │ │ └── TEa6b (786)
│ │ ├── VIS (669)
│ │ │ ├── VISal (402)
│ │ │ │ ├── VISal1 (1074)
│ │ │ │ ├── VISal2/3 (905)
│ │ │ │ ├── VISal4 (1114)
│ │ │ │ ├── VISal5 (233)
│ │ │ │ ├── VISal6a (601)
│ │ │ │ └── VISal6b (649)
│ │ │ ├── VISam (394)
│ │ │ │ ├── VISam1 (281)
│ │ │ │ ├── VISam2/3 (1066)
│ │ │ │ ├── VISam4 (401)
│ │ │ │ ├── VISam5 (433)
│ │ │ │ ├── VISam6a (1046)
│ │ │ │ └── VISam6b (441)
│ │ │ ├── VISl (409)
│ │ │ │ ├── VISl1 (421)
│ │ │ │ ├── VISl2/3 (973)
│ │ │ │ ├── VISl4 (573)
│ │ │ │ ├── VISl5 (613)
│ │ │ │ ├── VISl6a (74)
│ │ │ │ └── VISl6b (121)
│ │ │ ├── VISli (312782574)
│ │ │ │ ├── VISli1 (312782578)
│ │ │ │ ├── VISli2/3 (312782582)
│ │ │ │ ├── VISli4 (312782586)
│ │ │ │ ├── VISli5 (312782590)
│ │ │ │ ├── VISli6a (312782594)
│ │ │ │ └── VISli6b (312782598)
│ │ │ ├── VISp (385)
│ │ │ │ ├── VISp1 (593)
│ │ │ │ ├── VISp2/3 (821)
│ │ │ │ ├── VISp4 (721)
│ │ │ │ ├── VISp5 (778)
│ │ │ │ ├── VISp6a (33)
│ │ │ │ └── VISp6b (305)
│ │ │ ├── VISpl (425)
│ │ │ │ ├── VISpl1 (750)
│ │ │ │ ├── VISpl2/3 (269)
│ │ │ │ ├── VISpl4 (869)
│ │ │ │ ├── VISpl5 (902)
│ │ │ │ ├── VISpl6a (377)
│ │ │ │ └── VISpl6b (393)
│ │ │ ├── VISpm (533)
│ │ │ │ ├── VISpm1 (805)
│ │ │ │ ├── VISpm2/3 (41)
│ │ │ │ ├── VISpm4 (501)
│ │ │ │ ├── VISpm5 (565)
│ │ │ │ ├── VISpm6a (257)
│ │ │ │ └── VISpm6b (469)
│ │ │ └── VISpor (312782628)
│ │ │ ├── VISpor1 (312782632)
│ │ │ ├── VISpor2/3 (312782636)
│ │ │ ├── VISpor4 (312782640)
│ │ │ ├── VISpor5 (312782644)
│ │ │ ├── VISpor6a (312782648)
│ │ │ └── VISpor6b (312782652)
│ │ └── VISC (677)
│ │ ├── VISC1 (897)
│ │ ├── VISC2/3 (1106)
│ │ ├── VISC4 (1010)
│ │ ├── VISC5 (1058)
│ │ ├── VISC6a (857)
│ │ └── VISC6b (849)
│ └── OLF (698)
│ ├── AOB (151)
│ │ ├── AOBgl (188)
│ │ ├── AOBgr (196)
│ │ └── AOBmi (204)
│ ├── AON (159)
│ ├── COA (631)
│ │ ├── COAa (639)
│ │ └── COAp (647)
│ │ ├── COApl (655)
│ │ └── COApm (663)
│ ├── DP (814)
│ ├── MOB (507)
│ ├── NLOT (619)
│ │ ├── NLOT1 (260)
│ │ ├── NLOT2 (268)
│ │ └── NLOT3 (1139)
│ ├── PAA (788)
│ ├── PIR (961)
│ ├── TR (566)
│ └── TT (589)
│ ├── TTd (597)
│ └── TTv (605)
└── CTXsp (703)
├── BLA (295)
│ ├── BLAa (303)
│ ├── BLAp (311)
│ └── BLAv (451)
├── BMA (319)
│ ├── BMAa (327)
│ └── BMAp (334)
├── CLA (583)
├── EP (942)
│ ├── EPd (952)
│ └── EPv (966)
├── LA (131)
└── PA (780)
The structures attribute is a custom dictionary that can be queried by region number or acronym, and contains all the information for a given structure:
pprint(atlas.structures["root"])
{'acronym': 'root',
'id': 997,
'mesh': None,
'mesh_filename': PosixPath('/home/runner/.brainglobe/allen_mouse_100um_v1.2/meshes/997.obj'),
'name': 'root',
'rgb_triplet': [255, 255, 255],
'structure_id_path': [997]}
In particular, the structure_id_path key contains a list description of the path in the hierarchy up to a particular region, and can be used for queries on the hierarchy.
print(atlas.structures["CH"]["structure_id_path"])
[997, 8, 567]
We can use the atlas.get_structure_descendants and atlas.get_structure_ancestors methods to explore the hierarchy:
atlas.get_structure_descendants("VISC")
['VISC1', 'VISC2/3', 'VISC4', 'VISC5', 'VISC6a', 'VISC6b']
atlas.get_structure_ancestors("VISC6a")
['root', 'grey', 'CH', 'CTX', 'CTXpl', 'Isocortex', 'VISC']
Region masks#
Sometimes, we might want to have the mask for a region that is not labelled in the annotation stack as all its voxels have the number of some lower level parcellation in the hierarchy (concretely, if the brain is divided in hindbrain, midbrain, and forebrain, annotation == root_id will be all False).
To get the mask for a region, use
mask = atlas.get_structure_mask(997)
plt.imshow(mask[middle_section,:,:], cmap="gray")
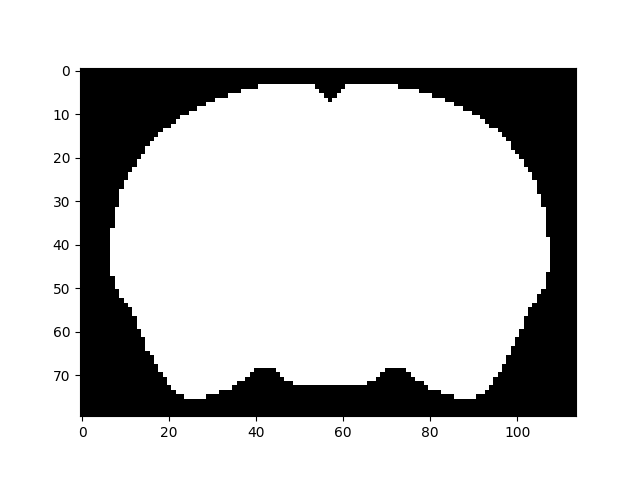
<matplotlib.image.AxesImage object at 0x7f927143eae0>
Region meshes#
To access the 3D structure mesh for visualisation, this can be queried using the region ID or abbreviation. A meshio.Mesh object is returned.
print(atlas.mesh_from_structure("CH"))
<meshio mesh object>
Number of points: 56703
Number of cells:
triangle: 112948
Point data: obj:vn
Cell data: obj:group_ids
A list of regions can also be queried:
pprint(atlas.mesh_from_structure(["CH", "VISp"]))
[<meshio mesh object>
Number of points: 56703
Number of cells:
triangle: 112948
Point data: obj:vn
Cell data: obj:group_ids,
<meshio mesh object>
Number of points: 3532
Number of cells:
triangle: 7056
Point data: obj:vn
Cell data: obj:group_ids]
The path can also be queried directly, if it’s needed to be used within another library
print(atlas.meshfile_from_structure("CH"))
/home/runner/.brainglobe/allen_mouse_100um_v1.2/meshes/567.obj
Querying the atlas#
A convenient feature of the BrainGlobeAtlas is being able to querying the identity of the structure at a given location, either from stack indexes or atlas coordinates.
Ask for identity of some indexes in the stack:
print(atlas.structure_from_coords((50, 40, 30)))
672
Now with coordinates in microns (and also returning the region acryonym):
print(atlas.structure_from_coords((5000, 4000, 3000), microns=True, as_acronym=True))
CP
Query at a specific level of the hierarchy:
print(atlas.structure_from_coords((5000, 4000, 3000), microns=True, hierarchy_lev=2, as_acronym=True))
CH
Querying the hemisphere#
A very similar method can be used for hemispheres. 0 correspond to outside the brain, and 1 and 2 to left and right hemispheres, but we can ask for the hemisphere name instead of the number:
Ask for the hemisphere of some indexes in the stack:
print(atlas.hemisphere_from_coords((50, 40, 30)))
2
Now give coordinates in microns
print(atlas.hemisphere_from_coords((5000, 4000, 3000), microns=True))
2
Now print hemisphere string
print(atlas.hemisphere_from_coords((5000, 4000, 3000), microns=True, as_string=True))
right
Total running time of the script: (0 minutes 17.706 seconds)